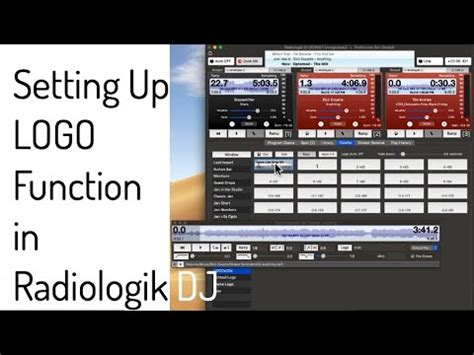
Calculate true position

Author: m | 2025-04-24

Calculated (ACTUAL) Radius True Position - The calculated radius offset see Spherical True Position Calculator. Calculated (ACTUAL) Spherical True Position - The calculated spherical positional tolerance diameter zone (2 x R). Related Resources: True Position GD T Tolerance Calculator; Tolerance Calculator Floating Fastener Condition

True-Position-Calculator/True Position Calculator.xlsx at

Orbit position become much larger when used for position calculation on Earth.Error Type: ClockRange: ± 2 mTiming drift – due to the distances, tiny timing errors in satellite clock accuracy become much larger errors on Earth.Error Type: MultipathRange: ± 1 mSignal replication due to reflection off objects such as buildings and terrain.Error Type: TroposphericRange: ± 0.5 mSignal propagation delay – lower atmosphere is far denser than other atmospheric layers and can refract radio waves.Error Type: Receiver noiseRange: ± 0.3 mGNSS receiver hardware and software induced signal noise that affects accuracy of perceived signal.The above sources of error can be broadly categorized as effects that delay the signal, and thus cause issues with the timing of the signal reception. For example, when receiving a reflected signal and not the original line-of-sight signal, which is common in dense urban areas due to tall buildings that create “urban canyons”. Of course, a complete blockage of the signal, such as when in a tunnel, underground or underwater results in a complete loss of all satellite signals.Highly sophisticated, modern GNSS receivers can deftly handle some of these issues using elegant mathematical techniques to determine the types of errors being encountered and applying offsets or corrections as required. Some of these capabilities are making their way into the lower cost, commodity GNSS receivers, such as those found in mobile phones. Despite having the capacity to correct some signal reception errors, when there is a complete loss of all satellite signals, the only real solution is to incorporate an inertial navigation system (INS) to estimate position calculations whilst inside the tunnel. This is known as dead-reckoning.GNSS Base Stations and Error Correction SolutionsSeveral ways of improving GNSS accuracy have been implemented outside of improving the performance of GNSS receivers. The primary means is through the installation of ground base stations that serve as on-Earth references for GNSS. The goal of base stations and GNSS error correction services is to establish the true path of the GNSS receiver, or as close to its true path as possible, in relation to an absolute position on the Earth’s surface.The base station receives GNSS signals and uses sophisticated measurement techniques to precisely calculate distances to observable satellites and thus to calculate GNSS signal errors; for example, ionospheric delay. All measurement and error correction data made at each base station is logged and archived. This data is used for various error correction solutions, Hello Was wondering if it's easy to calculate the True Position of a hole which is on an angled surface eg on 45degree using manual method? I know this can be done on PCDMIS automatically but was wondering if anybody knew how to do manually by hand? Thanks The equation will be the same as long as the data are transformed to the appropriate coordinate system. if you have a blueprint that makes geometric sense as well as the correct inspection equipment for the job you can certainly do plate layout and check a hole manually without a CMM The equation will be the same as long as the data are transformed to the appropriate coordinate system. What Jacob says. I can use this formula as in picture? I can use this formula as in picture? {"data-align":"none","data-size":"full","title":"True_Position_Calculation.JPG","data-attachmentid":495226} if you are measuring a true position with two axes being considered as basic, yes this is the correct formula. Sorry for all questions how about like in picture below... Do I need UVW data? sorry I'm complete noob at everything... You will need vectors, yes - unless you have translated the alignment so you are "looking down" the hole (like the image you posted earlier). If you don't use vectors (nom and actual) and you haven't rotated the alignment as explained, the result won't be perpendicular to the centerline.

True-Position-Calculator/True Position Calculator.xlsx at main

= y EndIf Shapes.Move(shp["obj"], grp["x"] + x, grp["y"] + y) Shapes.Rotate(shp["obj"], shp["angle"] + grp["angle"]) shape[i] = shp EndFor i = Stack.PopValue("local") grp["shape"] = shape group[i] = grp n = Stack.PopValue("local") y = Stack.PopValue("local") x = Stack.PopValue("local")EndSubSub Math_CartesianToPolar ' Math | convert cartesian coodinate to polar coordinate ' param x, y - cartesian coordinate ' return r, a - polar coordinate r = Math.SquareRoot(x * x + y * y) If x = 0 And y > 0 Then a = 90 ' [degree] ElseIf x = 0 And y a = -90 ElseIf x = 0 Then a = 0 Else a = Math.ArcTan(y / x) * 180 / Math.Pi EndIf If x a = a + 180 ElseIf x > 0 And y a = a + 360 EndIfEndSubSub SB_RotateWorkaround ' Small Basic | rotate workaround for Silverlight ' param shp - current shape ' param x, y - original coordinate ' param alpha - angle [radian] ' returns x, y - workaround coordinate If shp["func"] = "tri" Then x1 = -Math.Floor(shp["x3"] / 2) y1 = -Math.Floor(shp["y3"] / 2) ElseIf shp["func"] = "line" Then x1 = -Math.Floor(Math.Abs(shp["x1"] - shp["x2"]) / 2) y1 = -Math.Floor(Math.Abs(shp["y1"] - shp["y2"]) / 2) EndIf ox = x - x1 oy = y - y1 x = x1 * Math.Cos(alpha) - y1 * Math.Sin(alpha) + ox y = x1 * Math.Sin(alpha) + y1 * Math.Cos(alpha) + oyEndSubSub SB_Workaround ' Small Basic | workaround for Silverlight ' returns silverlight - "True" if in remote color = GraphicsWindow.GetPixel(0, 0) If Text.GetLength(color) > 7 Then silverlight = "True" msWait = 300 Else silverlight = "False" EndIfEndSubSub Shapes_CalcRotateZoomPos ' Shapes | calculate position for rotated and zoomed shape ' param["x"], param["y"] - position of a shape ' param["width"], param["height"] - size of a shape ' param ["cx"], param["cy"] - center of rotation ' param ["angle"] - rotate angle ' param ["scale"] - zoom scale ' return x, y - rotated position of a shape _cx = param["x"] + param["width"] / 2 _cy = param["y"] + param["height"] / 2 x = _cx - param["cx"] y = _cy - param["cy"] Math_CartesianToPolar(). Calculated (ACTUAL) Radius True Position - The calculated radius offset see Spherical True Position Calculator. Calculated (ACTUAL) Spherical True Position - The calculated spherical positional tolerance diameter zone (2 x R). Related Resources: True Position GD T Tolerance Calculator; Tolerance Calculator Floating Fastener Condition

True Position Calculator - Calculator Academy

Time your Exits with Average True Range (ATR) Trailing StopsThe ATR Trailing Stop is a stop loss system that adjusts according to the volatility of a trend and rachets up over time in order to lock in profits and protect capital. The stop trails behind price by a selected multiple of Average True Range (ATR).ATR Trailing Stops are primarily used to protect capital and lock in profits on individual trades, but--> They can also be used, in conjunction with a trend filter, to signal entries.Average True Range ("ATR") was introduced by J. Welles Wilder in his 1978 book New Concepts In Technical Trading Systems.ATR is a measure of volatility for a stock or index and is explained in detail at Average True Range.Wilder experimented with trend-following Volatility Stops using average true range.The system was subsequently modified to what is commonly known as ATR Trailing Stops.ATR Trailing Stop SignalsSignals are used for exits: Exit your long position (sell) when the price crosses below the ATR trailing stop line. Exit your short position (buy) when the price crosses above the ATR trailing stop line.While not conventional, they can also signal entries — in conjunction with a trend filter.ExampleThe RJ CRB Commodities Index's late 2008 downtrend is displayed with an Average True Range Trailing Stop (21 days, 3xATR, Closing Price) and a 63-day exponential moving average used as a trend filter.Mouse over chart captions to display trading signals. Go short [S] when the price closes below the ATR stop — while below the 63-day exponential moving average Exit [X] when the price crosses above the ATR stopseSetupTypical ATR time periods vary between 5 and 21 days. Wilder originally suggested using 7 days, short-term traders use 5, and longer-term traders use 21 days.Multiples between 2.5 and 3.5 x ATR are normally applied for trailing stops, with lower multiples more prone to whipsaws.The default is set as 3 x 21-day ATR.Closing Price is set as the default option. The alternative is HighLow (see Formula below).See Indicator Panel for directions on how to set up an indicator — and Edit Indicator Settings to change the settings.ATR Trailing Stops FormulaTrailing stops are normally calculated relative to the closing price: Calculate Average True Range ("ATR") Multiply ATR by your selected multiple — in our case 3 x ATR In an up-trend, subtract 3 x ATR from the Closing Price and plot the result as the stop for the Shutter speed 1/50 s.Flicker-free 60 Hz: The camera adjusts the aperture and gain automatically, and uses the shutter speed 1/60 s.Flicker-reduced: This is the same as flicker-free, but the camera might use shutter speeds faster than 1/100 s (50 Hz) and 1/120 s (60 Hz) for brighter scenes.Flicker-reduced 50 Hz: This is the same as flicker-free, but the camera might use shutter speeds faster than 1/100 s for brighter scenes.Flicker-reduced 60 Hz: This is the same as flicker-free, but the camera might use shutter speeds faster than 1/120 s for brighter scenes.Manual: The aperture, gain, and shutter are fixed.Exposure zone: Use exposure zones to optimize the exposure in a selected part of the scene, for example, the area in front of an entrance door.NoteThe exposure zones are related to the original image (unrotated), and the names of the zones apply to the original image. This means, for example, that if the video stream is rotated 90°, then the Upper zone becomes the Right zone in the stream, and Left becomes Lower.Automatic: Suitable for most situations.Center: Uses a fixed area in the center of the image to calculate the exposure. The area has a fixed size and position in the live view.Full: Uses the entire live view to calculate the exposure.Upper: Uses an area with a fixed size and position in the upper part of the image to calculate the exposure.Lower: Uses an area with a fixed size and position in the lower part of the image to calculate the exposure.Left: Uses an area with a fixed size and position in the left part of the image to calculate the exposure.Right: Uses an area with a fixed size and position in the right part of the image to calculate the exposure.Spot: Uses an area with a fixed size and position in

GD T True Position Calculator - Calculate GD T True Position

Vectors.wrap(pos)¶Puts a coordinate back into the box. If the coordinate is already in thebox, this function will return a new position vector that equals theoriginal vector.Return type:numpy.ndarrayReturns:A new position vector which is within the box. This functiondoes NOT mutate and return the input vector pos.isWithinCutoff(pos0, pos1, cutoff_sq)¶Return True if any of pos0 and pos1 are within the cutoff distance.Parameters:cutoff_sq (float) – = cutoff x cutoff__class__¶alias of builtins.type__delattr__¶Implement delattr(self, name).__dict__ = mappingproxy({'__module__': 'schrodinger.application.desmond.packages.analysis', '__init__': , 'box': , 'volume': , 'inv_box': , 'calcMinimumImage': , 'calcMinimumDiff': , 'wrap': , 'isWithinCutoff': , '__dict__': , '__weakref__': , '__doc__': None})¶__dir__() → list¶default dir() implementation__eq__¶Return self==value.__format__()¶default object formatter__ge__¶Return self>=value.__getattribute__¶Return getattr(self, name).__gt__¶Return self>value.__hash__¶Return hash(self).__init_subclass__()¶This method is called when a class is subclassed.The default implementation does nothing. It may beoverridden to extend subclasses.__le__¶Return self__lt__¶Return self__module__ = 'schrodinger.application.desmond.packages.analysis'¶__ne__¶Return self!=value.__new__()¶Create and return a new object. See help(type) for accurate signature.__reduce__()¶helper for pickle__reduce_ex__()¶helper for pickle__repr__¶Return repr(self).__setattr__¶Implement setattr(self, name, value).__sizeof__() → int¶size of object in memory, in bytes__str__¶Return str(self).__subclasshook__()¶Abstract classes can override this to customize issubclass().This is invoked early on by abc.ABCMeta.__subclasscheck__().It should return True, False or NotImplemented. If it returnsNotImplemented, the normal algorithm is used. Otherwise, itoverrides the normal algorithm (and the outcome is cached).__weakref__¶list of weak references to the object (if defined)class schrodinger.application.desmond.packages.analysis.Vector(msys_model, cms_model, from_xid, to_xid)¶Bases: schrodinger.application.desmond.packages.staf.GeomAnalyzerBaseCalculate the vector between two xids. Result is a vector for eachtrajectory frame.__init__(msys_model, cms_model, from_xid, to_xid)¶__call__()¶Call self as a function.__class__¶alias of builtins.type__delattr__¶Implement delattr(self, name).__dict__ = mappingproxy({'__module__': 'schrodinger.application.desmond.packages.analysis', '__doc__': '\n Calculate the vector between two xids. Result is a vector for each\n trajectory frame.\n ', '__init__':

jporeg/True-Position-Calc: true position calculator - GitHub

And think from the next position.”The problem here is a practical one again. Sometimes, the obvious moves are wrong!When solving tactical exercises, you know there is something good in the position. If there is only one forceful-looking move, you might be tempted to go with it without thinking.But during the game, this isn’t true at all. There are positions where a move looks good but loses instantly.That’s why it is important that you only execute a move during training when you finish your full calculation process. This habit will eventually save you a lot of points during your games.Wisdom from Artur JussupowArtur Jussupow, the former World #3 and my Coach in my teenage years, had some great advice when I used the shallow thinking method in training.A common conversation would go like that:Artur: “Solve this position, White to move, you get 5 MinutesNoël (after 30 seconds): “I believe f5 looks good.”Artur: “You can believe in the church; in chess, we calculate and know.”He would then not say anything until I came up with the full line I calculated until the very end.Since then, whenever I thought, “This move looks good,” I was reminded of Artur telling me to finish my calculation before making assumptions.The Road to Success: How to Solve Chess Puzzles CorrectlyNow that you know what to avoid solving a puzzle correctly is pretty straightforward. Open up your puzzle book or go to your favorite Online Chess Tactics Trainer.Now follow these three simple steps:1) Carefully examine the position before jumping into one move that looks or feels right (sometimes my students miss that they are material up or down because they immediately try to spot the right move).2) Come up with a List of Candidate moves. The simplest way to get the most forcing ones it to look for:ChecksCapturesThreatsin. Calculated (ACTUAL) Radius True Position - The calculated radius offset see Spherical True Position Calculator. Calculated (ACTUAL) Spherical True Position - The calculated spherical positional tolerance diameter zone (2 x R). Related Resources: True Position GD T Tolerance Calculator; Tolerance Calculator Floating Fastener Condition

True Position Axis Measurements Do Not Calculate to True Position

CALCULATOR : Bernoulli Equation Gas Pipeline Energy Grade Line EGL From Data Points [FREE] ± Calculate the Bernoulli equation total pressure or EGL (energy grade line) and pressure loss from data points for gas flow. Enter data points as three values separated by commas (position X, elevation Z, static pressure P) with each set of data on a new line. The position data should be in ascending order from the pipeline inlet to the pipeline outlet. Static pressure is gauge pressure (change units on the setup page). Select a data point to calculate the pressure terms at that data point (default is the pipe inlet). The total pressure or Bernoulli pressure equals the sum of the potential pressure, the static pressure and the dynamic pressure. For pipelines with constant diameter, the friction pressure loss is equal to the difference in total pressure. Note : The data point option is set to pipe inlet when the page loads. Click calculate to update the data point options to include all of the data points, then you select the data point. Click calculate each time you change the position data (X) values, and before you select the data point. Use the Result Plot option to plot the static pressure, dynamic pressure, potential pressure, hydraulic pressure and total pressure versus position. Use the Result Table option to display a table of static pressure, potential pressure, hydraulic pressure, delta hydraulic pressure and delta pressure per length versus data point. Tool Inputschdtype : Pipe Schedule Typediamtype : Pipe Diameter TypeODu : User Defined Outside DiameterIDu : User Defined Inside Diameterwtntype : Wall Thickness Typetnu : User Defined Wall Thicknessfluidtype : Fluid TypeSGu : User Defined Gas Specific Gravityzfactype : Compressibility Factor Typezu : User Defined Compressibility Factordatatype : Data Point (Click Calculate To Update)Xdata : Position Data PointsZdata : Elevation Data PointsPdata : Static Pressure Data PointsT : TemperatureNg : Mole FlowrateTool OutputID : Inside Diameter Pb : Bernoulli Pressure At Data PointPbΔ : Pressure Loss (From Inlet)Pbo : Bernoulli Pressure At InletPd : Dynamic Pressure At Data PointPh : Hydraulic Pressure At Data PointPhΔ/d : Pressure Loss Per LengthPs : Static Pressure At Data PointPz : Potential Pressure At Data PointSG : Gas Specific GravityZΔ : Delta Elevation d : Distance From Pipe Inlet z : Compressibility Factor CALCULATOR : Bernoulli Equation Gas Density And Compressibility Factor [FREE] ± Calculate Bernoulli equation gas density and